Buffer Zones Delimitation

January 21, 2019

Last year I had to solve the problem of defining buffer zones around a set of given points. Initially, a tessellation was a solution good enough. There is already some functionality in scipy to define Voronoi Tessellations. However, I needed to get the corresponding polygons in a specific format so that I could do some operation with them (for example aggregate observations per polygon or check for intersections with other polygons I had already defined). To solve this problem I wrote the function below.

import numpy as np
import geopandas as geop
from shapely import geometry
from shapely.ops import polygonize
from scipy.spatial import Voronoi

def voronoi_polygons(X, margin=0):
    '''
    Returns a set of Voronoi polygons corresponding to a set of points X.

    :param X: Array of points (optional).
              Numpy array, shape = [n, 2].

    :param margin: Minimum margin to extend the outer polygons of the tessellation.
                   Non-negative float.

    :return: Geopandas data frame.
    '''
    assert isinstance(X, np.ndarray), 'Expecting a numpy array.'
    assert X.ndim == 2, 'Expecting a two-dimensional array.'
    assert X.shape[1] == 2, 'Number of columns is different from expected.'
    n_points = X.shape[0]

    c1, c2 = np.sort(X[:, 0]), np.sort(X[:, 1])
    _diffs = np.array([max(margin, np.diff(c1).mean()), max(margin, np.diff(c2).mean())])

    min_c1, min_c2 = X.min(0) - _diffs
    max_c1, max_c2 = X.max(0) + _diffs

    extra_points = np.vstack([np.vstack([np.repeat(min_c1, n_points), c2]).T,
                              np.vstack([np.repeat(max_c1, n_points), c2]).T,
                              np.vstack([c1, np.repeat(min_c2, n_points)]).T,
                              np.vstack([c1, np.repeat(max_c2, n_points)]).T])

    _X = np.vstack([X, extra_points])

    # Define polygons geometry based on tessellation
    vor = Voronoi(_X)
    lines = [geometry.LineString(vor.vertices[li]) for li in vor.ridge_vertices if -1 not in li]
    disord = geometry.MultiPolygon(list(polygonize(lines)))
    ix_order = np.array([[i for i, di in enumerate(disord) if di.contains(geometry.Point(pi))]
                         for pi in X]).ravel()

    return geop.GeoDataFrame({'geometry': geometry.MultiPolygon([disord[i] for i in ix_order])})

The first lines of this function check the inputs. Since this code is part of a larger framework, I need to make this kind of checks at different points to spot where things break (if the do). The next part of the code consists of adding some extra points around the original set of points X. This is just to have a nicer tessellation. The last part of the code is about adding the polygons of interest to a GeoPandasDataframe.

Let's see how this works. We first generate 20 random points in a 2-dimensional space and then call the voronoi_polygons command. The result is a Geopandas data frame.

>>> num_points = 20
>>> X = np.random.uniform(0, 10, 2*num_points).reshape(num_points, 2)
>>> V = voronoi_polygons(X)
>>> V.head()
                                           geometry
0	POLYGON ((5.684519055982738 4.530960210050785,...
1	POLYGON ((4.393718709663499 8.131947355477712,...
2	POLYGON ((4.393718709663499 8.131947355477712,...
3	POLYGON ((1.510069716255606 8.207245127671737,...
4	POLYGON ((8.963549840344935 2.0485500981041, 8...

Below is an image of the tessellation. The command plot_buffer, used to generate this figure, is defined the end of this post.

>>> plot_buffer(X, V, title='Voronoi Polygons')
>>> plt.show()

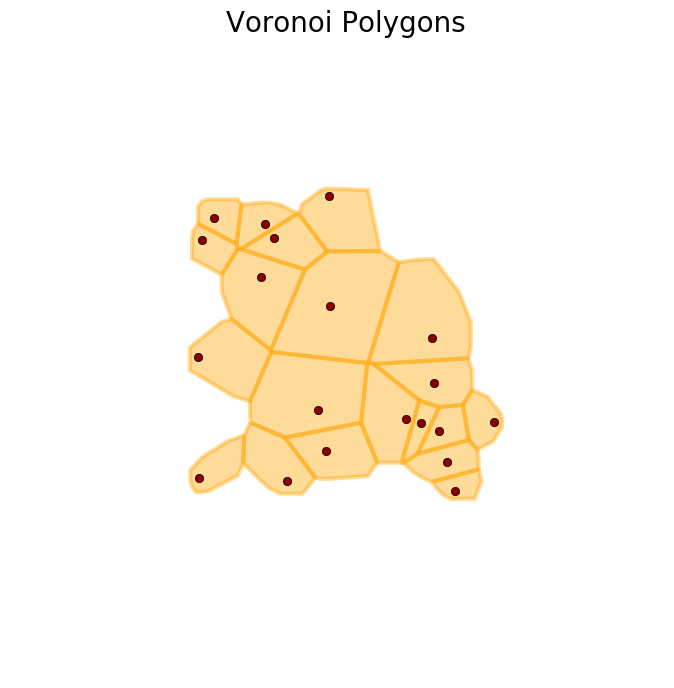
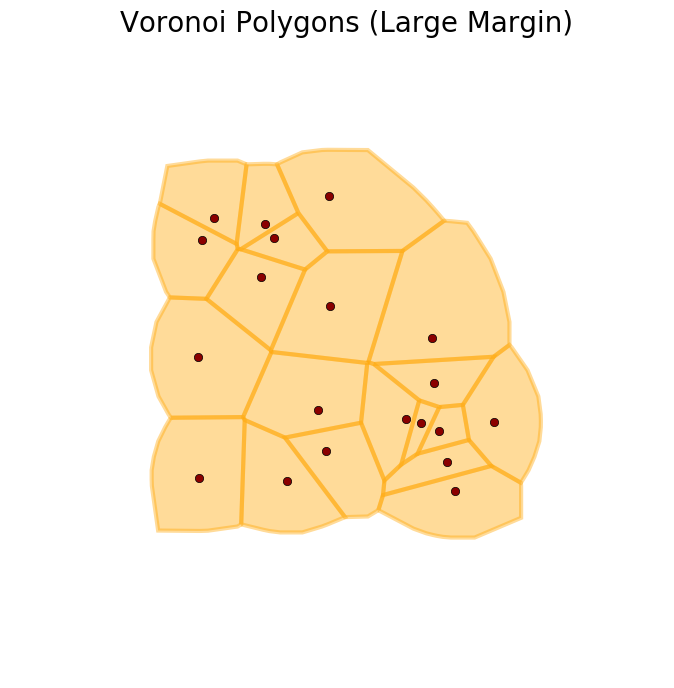
We can increase the extent of the tiles with the argument margin, as shown below.

>>> V = voronoi_polygons(X, margin=3)
>>> plot_buffer(X, V, title='Voronoi Polygons with a larger margin')
>>> plt.show()

The tessellation was fine for some applications, but there were other cases where the area of the tiles was just too large for some of the points. It was better to compute a regular polygon around the points instead. This function does this for us.

def regular_polygons(X, radius, n_angles=8):
    '''
    Return a set of regular polygons around points X.

    :param X: Array of points (optional).
              Numpy array, shape = [n, 2].

    :param radius: Circumradius of the polygon.
                   Positive float.

    :param n_angles: Number of angles of each polygon.
                     Integer >= 3.

    :return: Geopandas data frame.
    '''
    assert isinstance(X, np.ndarray), 'Expecting a numpy array.'
    assert X.ndim == 2, 'Expecting a two-dimensional array.'
    assert X.shape[1] == 2, 'Number of columns is different from expected.'

    assert isinstance(n_angles, int), 'n_angles must be an integer.'
    assert n_angles >= 3, 'Angles must be greater than two.'

    vertex = np.pi * np.linspace(0, 2, n_angles + 1)

    if isinstance(radius, float):
        assert radius > 0, 'Radius must be positive.'
        polys = [np.vstack([xi + radius * np.array([np.cos(t), np.sin(t)]) for t in vertex]) for xi in X]
    else:
        assert isinstance(radius, np.ndarray), 'Expecting a numpy array.'
        assert radius.ndim == 1, 'Expecting a one-dimensional array.'
        assert radius.size == X.shape[0], 'Array size is different from expected.'

        polys = [np.vstack([xi + ri * np.array([np.cos(t), np.sin(t)]) for t in vertex]) for xi, ri in zip(X, radius)]

    return geop.GeoDataFrame({'geometry': geometry.MultiPolygon([geometry.Polygon(pi) for pi in polys])})

>>> R = regular_polygons(X, radius=1.5, n_angles=6) #An example with hexagons
>>> plot_buffer(X, R, title='Regular Polygons')
>>> plt.show()

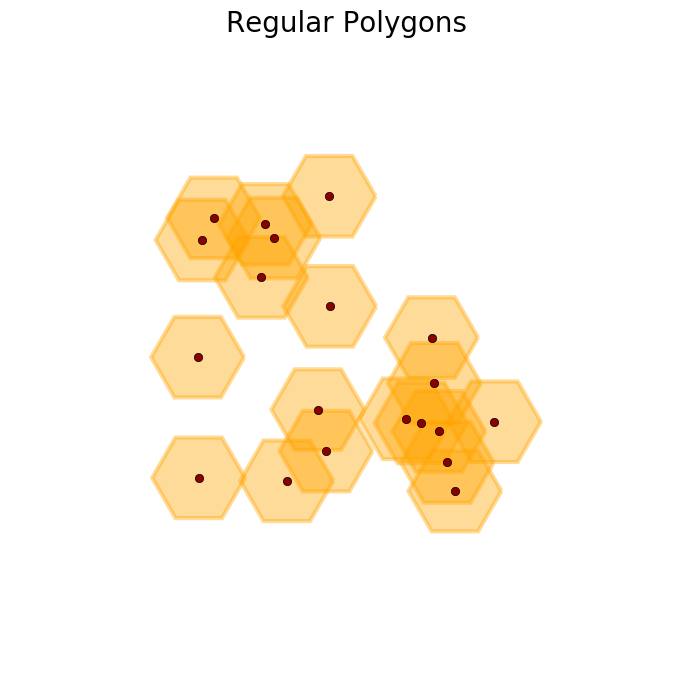
>>> R = regular_polygons(X, radius=1.5, n_angles=3) #An example with triangles
>>> plot_buffer(X, R, title='Regular Polygons')
>>> plt.show()

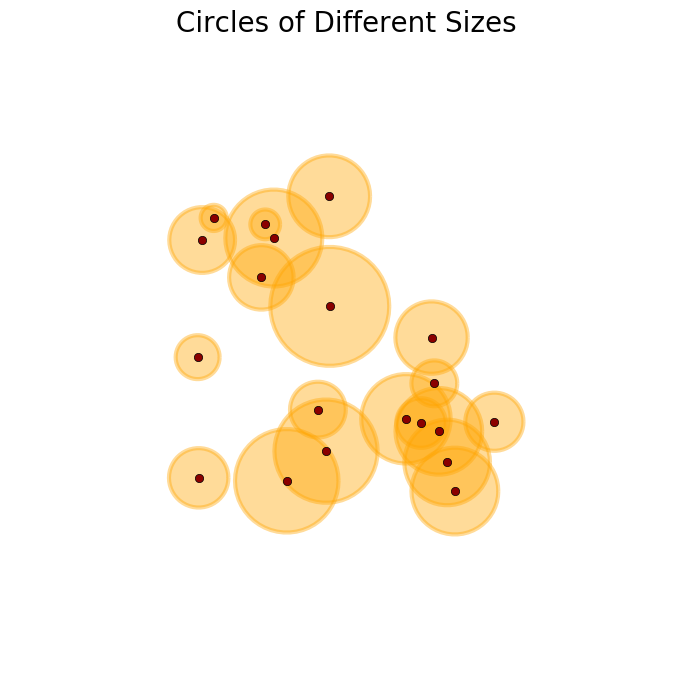
>>> R = regular_polygons(X, radius=np.random.uniform(.4, 2,X.shape[0]), n_angles=50) #Circles of different sizes
>>> plot_buffer(X, R, title='Circles of different sizes')
>>> plt.show()

So far so good, but then I was also requested to generate polygons that do not to overlap. This last task was easy, since now I only needed to combine the two functions above and define the following one.

def disjoint_polygons(X, radius, n_angles=8):
    '''
    Return a set of disjoint polygons around points X.

    :param X: Array of points (optional).
              Numpy array, shape = [n, 2].

    :param radius: Circumradius of the polygon.
                   Positive float.

    :param n_angles: Number of angles of each polygon.
                     Integer >= 3.

    :return: Geopandas data frame.
    '''
    vorpol = voronoi_polygons(X, margin=2*np.max(radius))
    regpol = regular_polygons(X, radius=radius, n_angles=n_angles)
    dispol = [vi.intersection(pi) for vi,pi in zip(vorpol.geometry, regpol.geometry)]

    return geop.GeoDataFrame({'geometry': geometry.MultiPolygon(dispol)})

>>> D = disjoint_polygons(X, radius=1.2, n_angles=10)
>>> plot_buffer(X, D, title='Disjoint Polygons')
>>> plt.show()

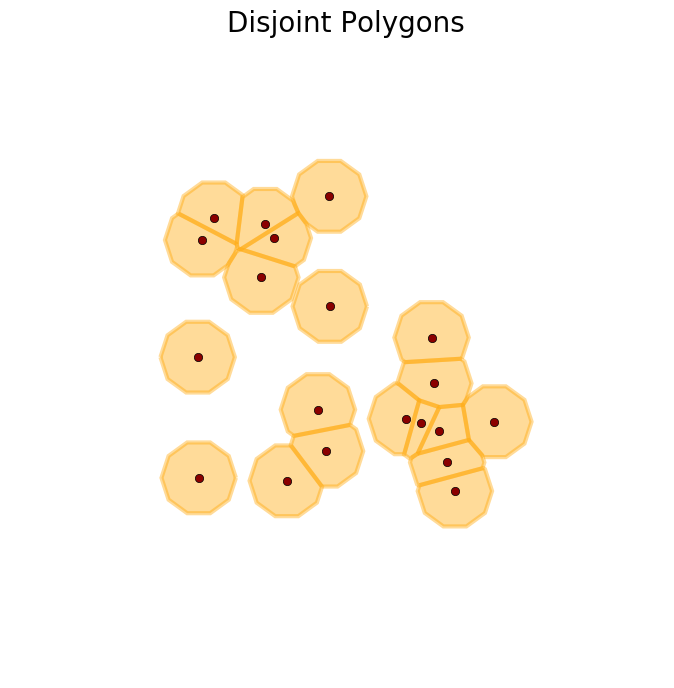
These are three ways of defining buffer zones that I wanted to share. I hope someone else finds them useful as well. This repository contains the code used here. The code for generating the figures in this post is the following.

from matplotlib import cm, colors, colorbar
from descartes import PolygonPatch
import matplotlib.pyplot as plt

def plot_buffer(X, G, title):
    fig, ax = plt.subplots(1, 1, figsize = (8, 8))
    ax.plot(*X.T, marker='o', color='darkred', lw=0)
    ax.set_title(title, size=20)
    ax.set_xlim(-5, 15)
    ax.set_ylim(-5, 15)
    for i, gi in enumerate(G.geometry): # Add continents
        ax.add_patch(PolygonPatch(gi, color='orange', ec='orange', lw=3, alpha=.4))
    ax.set_axis_off()